线性回归正则化
from:http://blog.csdn.net/cxmscb/article/details/53345795
损失函数
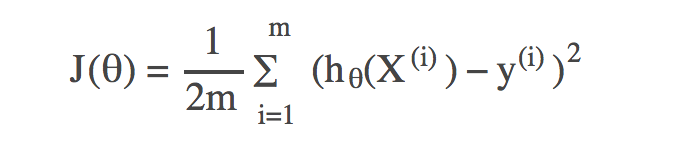
其中hθ(X)为需要学习到的函数,m为训练集样本的个数,Xi表示训练集中第i个样本的特征向量,yi表示第i个样本中的标签。
为了得到预测值hθ(Xi)和yi的绝对值,在公式上使用了平方数。为了平均每个样本的损失,在公式上对损失和进行除以m操作,,再除以2是为了之后的求导计算。
当我们的损失函数J(θ)在样本中损失较大时,会出现欠拟合的情况,即对样本的预测值和样本的实际结果值由较大的差距。
当我们的损失函数J(θ)在样本中损失约等于0 时,这时hθ(X)图像穿过样本的每一个点,这样会出现过拟合的情况,缺乏泛化能力,函数波动比较大,对待预测的样本预测能力比较弱。
对于过拟合问题,可以使用 正则化 的方法,即在原来的损失函数J(θ)上加上一个“尾巴”:
无正则化时的损失函数:
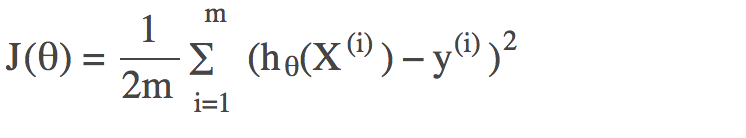
L1正则化下的损失函数:
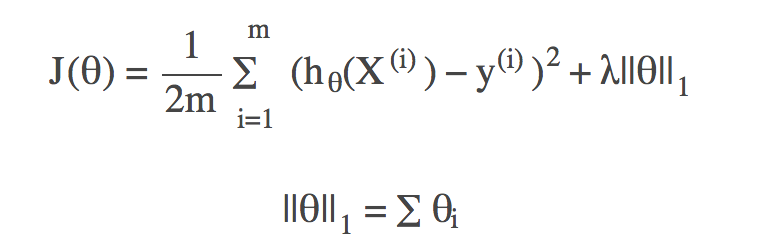
L2正则化下的损失函数:
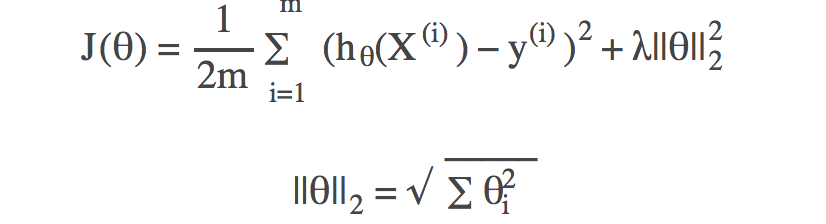
L1正则化、L2正则化也称为Lasso正则化、Ridge正则化,其中λ为模型的超参数。
正则化后的损失函数不仅要最小化预测值与样本点实际值间的差距了,还得最小化参数向量θ。当hθ(X)函数图像穿过所有样本点时,函数图像波动会非常大,(平方项、立方项等高次项的)的权重θi会很大,这样便会导致它的损失函数并非最小的。
正则化后,不仅要求hθ(X)接近更多的点,还要控制(高次项的)θi值,使得控制函数不能波动太大,而且正则化之后损失函数无法等于0。
L1正则化往往会使得一些θi值趋近于0(这可用于特征的选择),L2正则化往往会使得θi值之间差别不会太大,θi值之间的变化比较稳定。

