逻辑回归求解

LogisticRegression问题的常规步骤为：

Logistic回归一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），利用了Sigmoid函数，函数形式为：

对于线性边界的情况，线性回归的函数为：

所依，构造预测函数为：

函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

一般性，对于训练数据集，特征数据x={x1, x2, … , xm}和对应的分类数据y={y1, y2, … , ym}，对于单个样本，其后验概率为：

对于整个样本集，也就是n个独立的样本出现的似然函数为（因为每个样本都是独立的，所以n个样本出现的概率就是他们各自出现的概率相乘）

那最大似然法就是求模型中使得似然函数最大的系数取值θ*。这个最大似然就是我们的代价函数（cost function）了。

代价函数有了，我们下一步要做的就是优化求解了。我们先尝试对上面的代价函数求导，看导数为0的时候可不可以解出来，也就是有没有解析解，有这个解的时候，就皆大欢喜了，一步到位。如果没有就需要通过迭代了，耗时耗力。

最大似然估计就是要求得使l(θ)取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。

我们先变换下L(θ)：取自然对数，然后化简（不要看到一堆公式就害怕哦，很简单的哦，只需要耐心一点点，自己动手推推就知道了。注：有xi的时候，表示它是第i个样本，下面没有做区分了，相信你的眼睛是雪亮的），得到：

这时候，用L(θ)对θ求导，得到：

然后我们令该导数为0，你会很失望的发现，它无法解析求解。不信你就去尝试一下。所以没办法了，只能借助高大上的迭代来搞定了。这里选用了经典的梯度下降算法。

上述推导中，最大似然估计就是要求得使l(θ)取最大值时的θ，这里可以使用梯度上升法求解。我们稍微变换一下：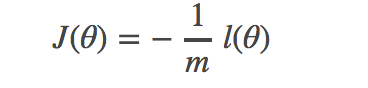

因为乘了一个负的系数−1/m，然后就可以使用梯度下降算法进行参数求解了。

上面推导中已经说明了使用梯度下降求解，具体就不在这里多说了，看下一章。

02：逻辑回归求解