线性回归算法模型

线性模式形式简单、易于建模，但却蕴含着机器学习中一些重要的基本思想，许多功能更为强大的飞线性模型可在线性模型的基础上通过引入层级结构或者高维映射得到。此外，由于w直观表达了各属性在预测中的重要性，因此线性模型有很好的可解释性，本章介绍经典的线性模式算法处理方式，然后讨论二分类问题和多分类问题。

损失函数

监督学习问题是在假设空间 中选取模型f作为决策函数，对于给定的输入X，由f(X)给出相应的输出Y，这个输出的预测值f(X)与真实值Y可能一致也可能不一致，用一个损失函数（loss function）或代价函数（cost function）来度量预测错误的程度。损失函数是f(X)和Y的非负实值函数，记作L(Y,f(X))。统计学习常用的损失函数有以下几种：

（1）0-1损失函数（0-1 loss function）

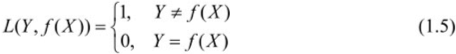
（2）平方损失函数（quadratic loss function）

3）绝对损失函数（absolute loss function）

(4）对数损失函数（logarithmic loss function）或对数似然损失函数（loglikelihood loss function）

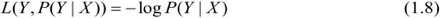
损失函数值越小，模型就越好。由于模型的输入、输出（X,Y）是随机变量，遵循联合分布P(X,Y)，所以损失函数的期望是

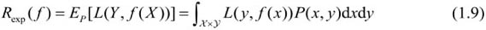
这是理论上模型f(X)关于联合分布P(X,Y)的平均意义下的损失，称为风险函数（risk function）或期望损失（expected loss）。

学习的目标就是选择期望风险最小的模型。

回归分析的平方损失

对于一元线性回归来说，可以看成Y的值是随着X的值变化，每一个实际的X都会有一个实际的Y值，我们叫Y实际，那么我们就是要求出一条直线，每一个实际的X都会有一个直线预测的Y值，我们叫做Y预测，回归线使得每个的实际值与预测值之差的平方和最小，即（Y1实际-Y1预测）^2+（Y2实际-Y2预测）^2+ …… +（Yn实际-Yn预测）^2的和最小。

我们能够给出单变量线性回归的模型：

我们常称x为feature，h(x)为hypothesis；

从上面“方法”中，我们肯定有一个疑问，怎么样能够看出线性函数拟合的好不好呢？

我们需要使用到Cost Function（代价函数），代价函数越小，说明线性回归地越好（和训练集拟合地越好），当然最小就是0，即完全拟合；

举个实际的例子：

我们想要根据房子的大小，预测房子的价格，给定如下数据集：

根据以上的数据集画在图上，如下图所示：

我们需要根据这些点拟合出一条直线，使得cost Function最小；

虽然我们现在还不知道Cost Function内部到底是什么样的，但是我们的目标是：给定输入向量x，输出向量y，theta向量，输出Cost值；

以上我们对单变量线性回归的大致过程进行了描述；

Cost Function

Cost Function的用途：对假设的函数进行评价，cost function越小的函数，说明拟合训练数据拟合的越好；

下图详细说明了当cost function为黑盒的时候，cost function 的作用；

但是我们肯定想知道cost Function的内部构造是什么？因此我们下面给出公式：

其中：

表示向量x中的第i个元素；

表示向量y中的第i个元素；

表示已知的假设函数；

m为训练集的数量；

如果theta0 一直为 0， 则theta1与J的函数为：

如果有theta0与theta1都不固定，则theta0、theta1、J 的函数为：

当然我们也能够用二维的图来表示，即等高线图；

的函数一定是碗状的，即只有一个最小点；

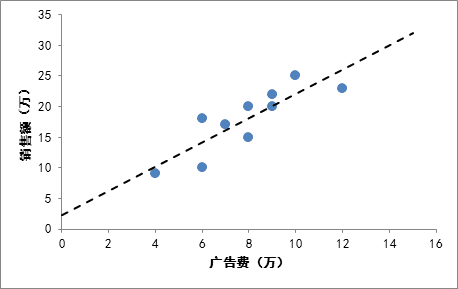
现在来实际求一下这条线：

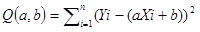
我们都知道直线在坐标系可以表示为Y=aX+b，所以（Y实际-Y预测）就可以写成（Y实际-（aX实际+b）），于是平方和可以写成a和b的函数。只需要求出让Q最小的a和b的值，那么回归线的也就求出来了。

均方误差有非常好的几何意义，它对应了常用的欧几里得距离或简称“欧氏距离”，基于均分误差来求解最小化模型的方法称为“最小二乘法(least square method)”。在线性回归中，最小二乘法就是试图找到一条直线，使所有的样本到直直线上的欧氏距离之和最小。

首先，一元函数最小值点的导数为零，比如说Y=X^2，X^2的导数是2X，令2X=0，求得X=0的时候，Y取最小值。

那么实质上二元函数也是一样可以类推。不妨把二元函数图象设想成一个曲面，最小值想象成一个凹陷，那么在这个凹陷底部，从任意方向上看，偏导数都是0。

因此，对于函数Q，分别对于a和b求偏导数，然后令偏导数等于0，就可以得到一个关于a和b的二元方程组，就可以求出a和b了。下面是具体的数学演算过程，先把公式展开一下：

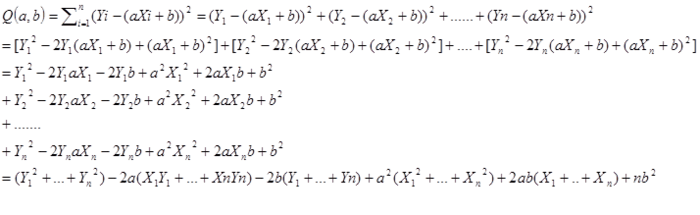
然后利用平均数，把上面式子中每个括号里的内容进一步化简。例如：

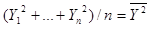
则：

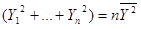
于是：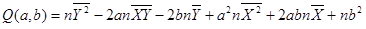

然后分别对Q求a的偏导数和b的偏导数，令偏导数等于0。

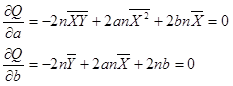
进一步化简，可以消掉2n，最后得到关于a，b的二元方程组为

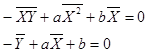
最后得出a和b的求解公式：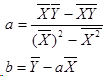

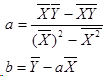
本次文章参考了：https://www.jianshu.com/p/fcd220697182#和周志华的机器学习

有了这个公式，对于广告费和销售额的那个例子，我们就可以算出那条拟合直线具体是什么，分别求出公式中的各种平均数，然后带入即可，最后算出a=1.98，b=2.25

最终的回归拟合直线为Y=1.98X+2.25，利用回归直线可以做一些预测，比如如果投入广告费2万，那么预计销售额为6.2万。

上面公式推导的是每个样本只有一个属性，不失一般性，假设样本有m个属性，回归方程为：

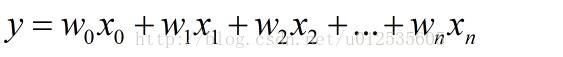
参照上述单变量的回归方程，经过对比发现该方程中缺少常数项，其实常数项是WoXo，测试的Xo等于1，为保持形式的一致性，同时偏于写成矩阵的形式，做了一个等价处理。

举证表示形式中，X和Y分别是：

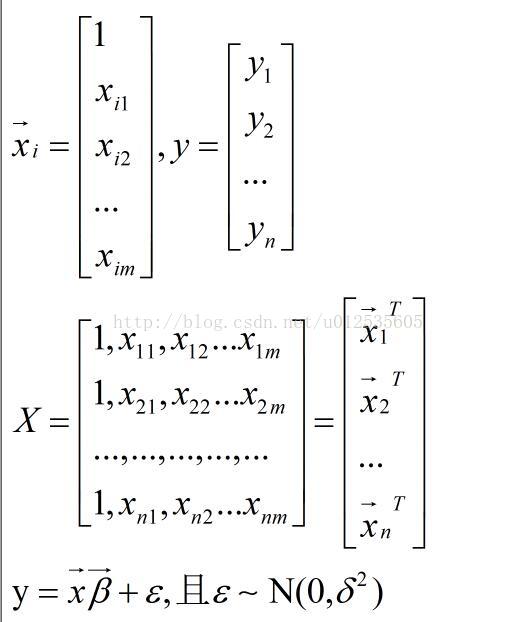
上述的推导过程比较详细，在周志华的机器雪中，关于使用矩阵表示的形式和推导过程附上如下：

单变量线性回归的情况很容易扩展到多变量的情况。在多变量线性回归中每一个输入有多个属性，即xj=(xj1, xj2, ..., xjd)，其模型变为：

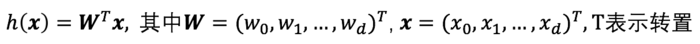
为了统一形式，我们引入一个哑输入属性x0，并令x0恒等于1。于是，上式可写为如下形式：

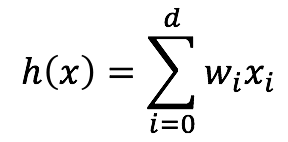
将其写成矩阵形式，可得下式：

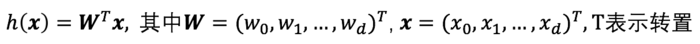
上面的式子都是对于一个输入x而言的，对于训练数据集中所有的m个输入，我们引入哑属性后，数据集中的属性应该是如下的形式：

x1=(1, x11, x12, ..., x1d)

x2=(1, x21, x22, ..., x2d)

x3=(1, x31, x32, ..., x3d)

……

xm=(1, xm1, xm2, ..., xmd)

可以用下面的矩阵X来表示数据集中所有的数据属性集合：

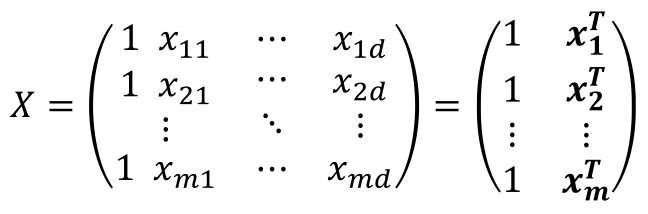
我们把所有的输出yj也写成向量向量形式：

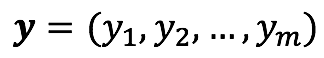
在多变量的情况下损失函数为：

按照矩阵运算规则，将损失函数写为矩阵形式：

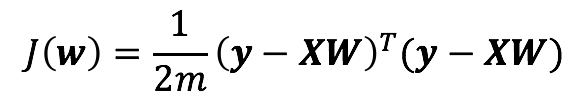
对W求导得：

令导数为0，可以解得解析解：

当XTX可逆时，XTX须为满秩（秩 为 n）。

X为m×n的矩阵，其秩为m和n中最小的一个数，为保证XTX满秩，m需大于n，即训练样本的个数需大于样本的特征维度。

至此单变量和多变量线性回归的情况就都讨论过了。

上面给出了单变量线性回归和多变量线性回归的解析解（有的书上也称闭式解），可以看出这种解析解计算原理简单。但是，在实际情况中我们常常无法按令偏导数为0的方法求出解析解，这是因为要么损失函数没有解析解，比如损失函数不是处处可导的函数；要么求解解析解太耗时，比如特征空间维度太高。另外，在多变量的情况下我们也可以看出，求解解析解要求X转置乘X可逆，实际中这个条件不一定满足，而且即便能满足，当矩阵的维度很高时求解解析解也是极为耗时。所以我们常常只能使用数值计算的方法求取近似的数值解，梯度下降法就是常用的数值计算的方法。Andrew NG在其课程中曾说过，即便是解析解存在，当特征超过10000维时，他也会考虑使用数值解，因为求解解析解太耗时了。关于梯度下降算法将放在下篇笔记中说明。

最后要说的是，单变量线性回归不必担心过拟合的问题，但是对于多变量线性回归我们需要考虑如何避免过拟合。实践中采用引入正则化项的办法来避免过拟合。

啥叫过拟合？在那些情况下，可能会过拟合？过拟合怎么办？正则项为什么可以防止过拟合？

过拟合是在训练样本上拟合的很好，但是在测试集上表现不好。说明模型过于复杂，可能充分拟合了训练样本上的噪声。拟合过于充分的话，说明在样本间曲线有很大的波动，则导数值很大，也就是系数很大。

训练集上数据量小，特征太多都有可能过拟合。

可增大数据量，减小特征，交叉验证，加入正则项

关于正则化的内容也会在下一节中说明。

由于周志华的机器学习这本书找不到电子版，所依关于该部分引用互联网：https://www.jianshu.com/p/c93a9211e447